A theory of scales. Probably a bit bonkers but ...
Scale electrics
A diatonic scale is 8 notes distributed over 12 semitones. There are many combinations for this:
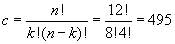
Most of these combinations make no musical sense. So what makes a scale work? One rule is it must consists of 5
tone intervals and 2 semitone intervals. But what determines the distribution and is it necessary to impose any rules for this structure to emerge?
I think the answer may be that the notes attempt to distribute evenly but 12 does not divide by 7 which leads to the
structure of scales and other artefacts like the circle of fifths. There is no need to impose the rule; 5 tones and 2 semitones, this emerges as having the
most stable structure.
Potential Energy
Imagine a string of eight beads on a wire of fixed and finite length. If each bead repels the other beads
according to some law r = R(d) where d is the distance from the centre of a bead to another bead then the beads will arrange themselves with equal
spacing between them. The form of the law is immaterial as long as it decays monotonically with distance. The equal spacing will represent the point of
lowest energy for the system.
So, if we assume the wire is of length 12, then the energy function will be of the form:
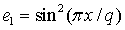
where
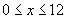 then the energy is at a minimum at 0, q, 2q, 3q, 4q, 5q, 6q, 7q where
then the energy is at a minimum at 0, q, 2q, 3q, 4q, 5q, 6q, 7q where
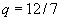 representing the 8 notes of a diatonic scale.
representing the 8 notes of a diatonic scale.
If however, the positions on the wire do not have equal potential energy, like for instance a wire that attracts
the beads to particular positions, then it is the interplay of these two potential energy fields that will determine the position of the beads.
If we model the position of the notes in a diatonic scale this way we can show that the scales that emerge are
the same as those that we use and they exist because they form a stable system.
So there are 12 notes in an octave, representing 11 intervals of 1 semitone (the details of Equal
Temperament versus Just Intonation and other tunings do not change this assumption).
There are 8 notes in a standard scale and 7 intervals. We are excluding pentatonic, chromatic, and other
exotica as these are all derived scales but the same principals still apply.
If we provide a field along the wire that provides the energy minima at the 12 points of the scale then how
will the scale notes distribute themselves to minimise the system's overall energy?
Assume the energy distribution along the wire is:
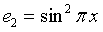
where 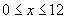 then the energy is at a minimum at 0,1,2,3,4,5,6,7,8,9,10,11,(12) representing the 12 semitones of a diatonic scale.
then the energy is at a minimum at 0,1,2,3,4,5,6,7,8,9,10,11,(12) representing the 12 semitones of a diatonic scale.
If we combine these two energy functions and provide some relative weighting then we get:
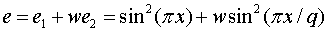
With w = 1 then the graph looks
like:
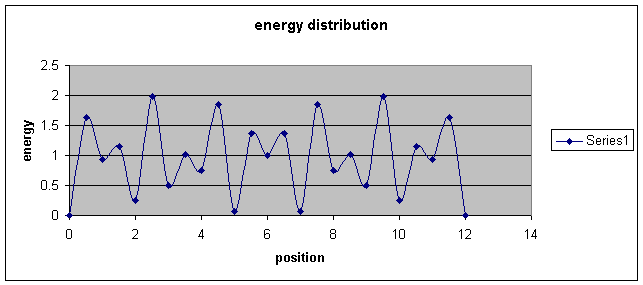
From the graph one can see that the most stable (with least energy) notes are at: 0,2,5,7,10 and 12
In scale of C Major we have:
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
1
|
|
2
|
|
3
|
4
|
|
5
|
|
6
|
7b
|
7
|
8
|
|
C
|
|
D
|
|
E
|
F
|
|
G
|
|
A
|
Bb
|
B
|
C
|
So these are the tonic, the 2nd, the perfect 4th, the perfect 5th, the flattened 7th and
the octave.
The others notes can take up a variety of positions but are less stable.
Also, the scale is symmetric about position 6 (flattened 5th) which is true of just the Ionian,
Dorian and Phrygian scales, that is the first three modal scales. If T=tone and
S=semitone the Ionian major scale is TTS T TTS and the Aeolian minor is TST T
STT.
If we take the 8 most stable notes from the graph we have TST T TST, which is the Dorian scale.
The other modal scales therefore all have slightly higher overall energy, which is an interesting result. The
Dorian scale is the first of the modal minor scales and is symmetric and does have a particularly pleasing sound.
So maybe the lower a scale's energy (ie stability) the more mellow. The higher the energy the more
challenging. On this basis you can order the modal scales by relative stability:
| Stability | Scale | Intervals |
| 1
| Dorian
| TST T TST
|
| 2
| Aeolian
| TST T STT
|
| 2
| Mixolydian
| TTS T TST
|
| 3
| Ionian
| TTS T TTS
|
| 4
| Phrygian
| STT T STT
|
| 5
| Lydian
| TTT S TTS
|
| 5
| Locrian
| STT S TTT
|
If you play each of these scales
in this order there does appear to be an increasing sense of tension?
Interestingly, the Ionian sits in the middle of the range of stability, not at
the top. From there you can head towards the mellow Dorian or to the jazzy
Locrian ?
Also, another observation is that
when resolving to the octave the sound that often provides the biggest sense of
resolution is the resolution of 7th
to the octave or the flattened 2nd to the tonic. From the graph,
both require the biggest energy change between two adjacent semitones.
It all sort of seems to work and to reflect reality...a bit ?!
And its all because 12 is not divisible by 7
12 * n is not divisible by 7 where n < 7
A fifth is 7 semitones. A fourth is 5 semitones.
So: 4th + 5th = octave
So to pass through all the notes in steps of 7 semitones you need to iterate
over the octave of 12 semitones 6 times picking the 2 notes (x and y) 7 or 5 semitones apart
x --> y = 7 or y --> x = 5
| |
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
| |
C
|
|
D
|
|
E
|
F
|
|
G
|
|
A
|
|
B
|
C
|
| 1
|
x
|
|
|
|
|
|
|
y
|
|
|
|
|
|
| 2
|
|
|
x
|
|
|
|
|
|
|
y
|
|
|
|
| 3
|
|
|
|
|
x
|
|
|
|
|
|
|
y
|
|
| 4
|
|
y
|
|
|
|
|
x
|
|
|
|
|
|
|
| 5
|
|
|
|
y
|
|
|
|
|
x
|
|
|
|
|
| 6
|
|
|
|
|
|
y
|
|
|
|
|
x
|
|
|
The Circle of 5ths is just an artefact of 12 not being divisible by 7.


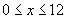 then the energy is at a minimum at 0, q, 2q, 3q, 4q, 5q, 6q, 7q where
then the energy is at a minimum at 0, q, 2q, 3q, 4q, 5q, 6q, 7q where
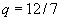 representing the 8 notes of a diatonic scale.
representing the 8 notes of a diatonic scale.